原文作者:Transmissions11、Frankie、Dave White,Paradigm
原文编译:Amber,Foresight News
相关阅读
《Paradigm 最新研究:一文读懂渐进式荷兰拍卖》
概述
本文将介绍一种全新的代币发行机制。可变利率的渐进式荷兰拍卖(VRGDA),专为Art Gobblers设计并在0xMonaco中使用,通过在销售情况好于预期时提高价格并在销售状况不佳时降低价格,让发行方能够在自定义的时间范围内获得预期的代币销售结果。
本文除了将阐述这一机制的详情以外,还会提供一个已经被高度优化且可以直接投入生产的Solidity实例,并给出一些案例的演示结果。
设计这一机制的动机
Art Gobblers是 Justin Roiland 和 Paradigm 共同推进的一场数字艺术领域的实验。该项目的一个重要目标是创建一个自给自足的生态系统,该生态系统可以在未来几年内实现在无需人工干预的状况下自行繁荣发展。
该系统中有两种核心NFT资产,团队希望通过合理的机制设计,让任何人在任何时刻都能够购买到NFT。思路就是一部分有发行上限的资产全部售出的同时,另一部分则保持恒定速率增发,这样无论用户在什么时间「入场」,都不必等待某一个时刻的集中拍卖,而随时都能买到相应的NFT资产。
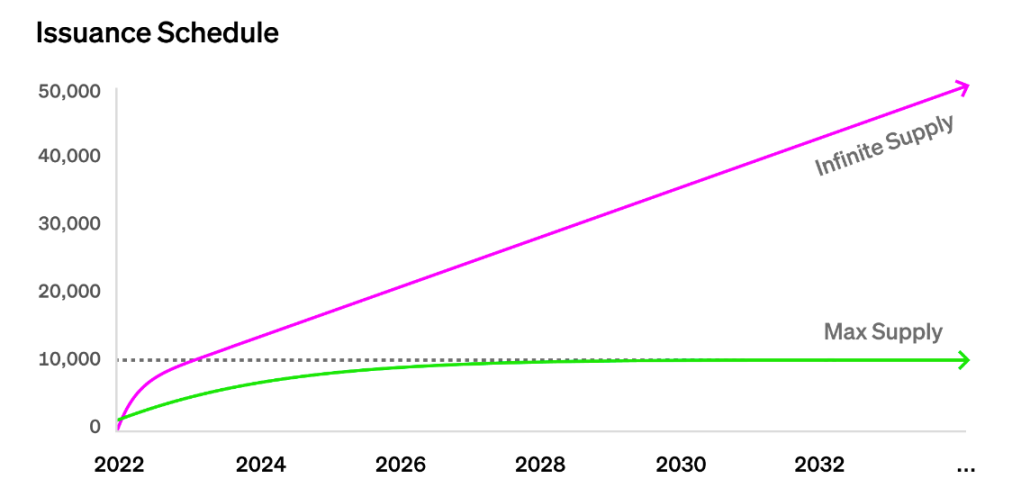
我们的解决方案就是 VRGDA,它是 GDA (渐进式荷兰拍卖)的一种泛化,允许高度定制化地调度 NFT 发行,而不是标准 GDA 的统一线性调度。
机制
设计思路
现在假设一个简单的时间表,我们希望每天售出 10 个 NFT。我们为第一个 NFT 设置了 1 个代币的起始价格。
假设现在是第 5 天,那么我们应该卖出了 50 个 NFT。但是,市场需求一直很高,我们已经卖出了 70 个。我们本来应该在第 7 天之前卖出 70 个 NFT,所以我们提前两天达成了这一销售目标。
因此,我们希望在未来调高NFT的出售价格。我们可以使用指数曲线来确定价格的调整幅度。这个参数怎么设置实际上可以有很多种选择,不过这里先用一个最简单的思路,既然我们比预期的销售达成日期提前了2天,那么就用2的2次方作为调整参数,即4,这意味着新的价格从1个代币变成了4个代币,市场需求相对稳定的状况下,价格的上涨自然会让销售进度有所减慢。
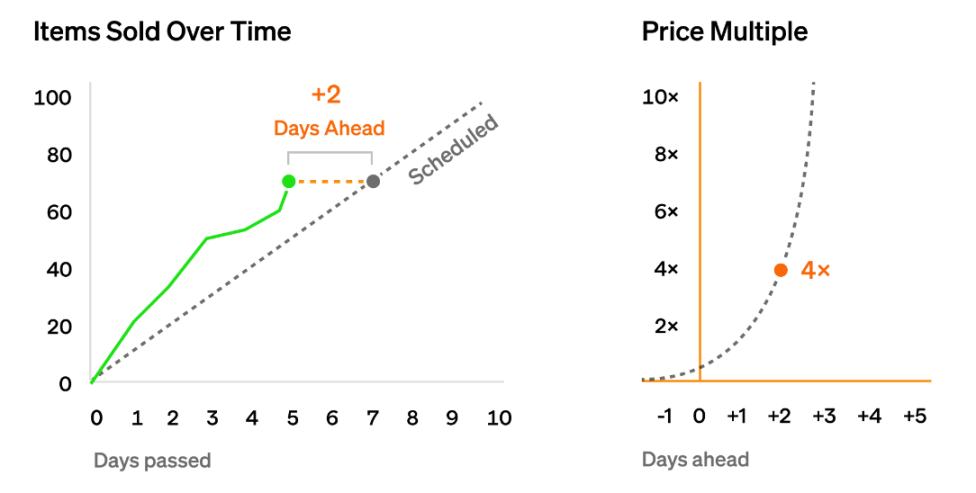
现在时间来到了10天以后,即开始销售的第15天,我们应该卖掉了150个NFT,但是用户只买走了120个,也就是说我们比原计划落后了三天,那么我们的价格调整参数就应该是2的-3次方,也就是0.125,简单来说就是一个NFT的单价从1个代币变成了0.125个代币,以此来刺激更多的用户买入。
建立模型
参数
- 如果 NFT 以完美的预定速度售出,NFT 的售价(目标价格)。
- 在没有购买的情况下,NFT 价格在单位时间内下降的百分比。
- 发行时间表:t时刻需要出售的 NFT 数量。
目标
我们希望按特定时间表发行 NFT。我们将使用的机制是,如果提前出售 NFT,则提高价格,如果落后于预定时间出售,则降低价格。如果销售完全按计划进行,购买下一个的价格将保持不变。
定义
假设我们想按照预定的时间表 出售 NFT,它将一个时间点t映射到我们当时想要出售的 NFT 的累积数量。例如,如果我们想每两天卖出一个 NFT,的定义就是:
假设我们想通过每个 NFT 的单独荷兰式拍卖来出售我们的 NFT。如果我们将每个 NFT 的起始价格设置为 1,并让该价格在没有销售发生的情况下以每单位时间 的速率衰减,这样如果在时间 购买NFT,它的价格就是:
为了提高灵活性,我们可以调整拍卖的起点,比如加一个参数 ,这样对应时间 的价格就会变成:
如果我们希望起始价格不是1,我们可以多乘一个常数 . 我们可以把调整后的价格定为 :
的定义
根据我们的发行时间表 , 我们想在时刻 卖出 个 NFT 。我们可以 通过反转 计算从卖出 个应该花费的时间定义 :
VRGDA 目标的一个结果是,如果第 个 NFT 根据其发行时间表在目标时间被准确购买,其价格将为 。 这意味着如果我们以准确的目标价格销售,那么在时间 ,第 个NFT 的定价如下:
如果不计算 ,那么简化的模型就是:
这意味着 或者 。 使用前文定义的 的概念,我们可以得出 .
最终公式
通过将 导入 ,我们最终得到最终公式:
简单的发行案例
下面我们演示推导一些简单的发行时间表以与 VRGDA 公式一起使用。
线性
假设我们要每天出售 个 NFT。这意味着 ,也就是
把 代入 VRGDA 定价公式,我们最终得到以下结果:
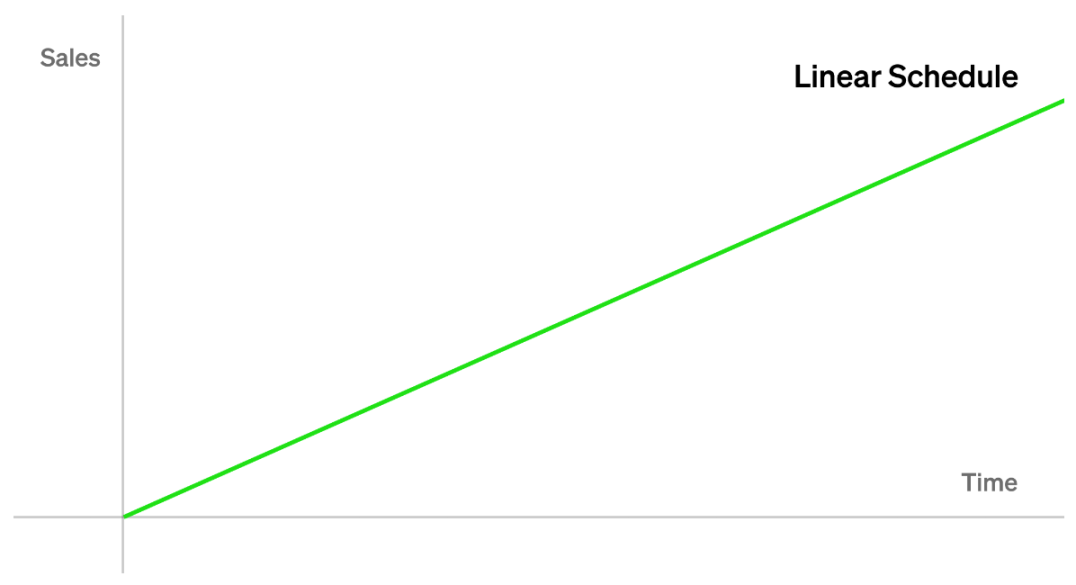
这种情况实际上与GDA是同构的,这就是我们称 VRGDA 为 GDA 的泛化的原因。
平方根
假设我们希望以与时间的平方根成正比的速率发行 NFT——例如,一开始发行 NFT 更快,然后随着时间的推移逐渐变慢,但永远不会停止。
然后我们可以设置 ,因此在第 1 天我们卖出了 1 个 NFT,在第 4 天我们要卖出 2 个,在第 9 天我们需要卖出 3 个,依此类推。
在这种情况下, 。现在我们只需代入 VRGDA 定价公式即可获得:
更复杂的释放逻辑
与上述示例相比,这部分会更复杂。然而,我们仍然选择详细介绍它,因为它提供了一种在不强制实施无限通货膨胀机制的情况下引导持续增长的方法。
动机
假设我们一开始想快速发行 NFT,然后放慢速度,直到最终被全部释放,就像 Art Gobblers 中的情况一样。
对此进行建模的一种简洁方法是使用具有正域的逻辑函数。
导出
逻辑函数是一个 S 形曲线。我们将其稍微简化并将其定义为:
这条曲线在 接近负无穷大时无限接近 0,而在 接近正无穷大时无限接近1。
对于我们的特定应用程序,我们不想使用完整的 S 曲线(尽管也可能有一个完整的逻辑 VRGDA,它会开始缓慢、加速,然后再次减速)。我们只想使用曲线的一部分。
因为虽然 ,但我们希望我们的时间表显示在时间 0 卖出 0 个 NFT,我们需要通过减去 0.5 来将此函数向下移动。这条新曲线的起始点将从 0 变为 0.5:
假定我们想发行 个NFTs,所以我们需要在这个函数中乘上一个因子 .
我们还可以引入时间参数 t调整发行 NFT 的速度:
参数的意义
基于上面的结果进行计算:
这意味着我们可以调整 决定我们希望发行大约 46% 的 NFT 的时间。例如,如果我们希望在 100 个时间单位后发行 46% 的 NFT,这意味着 ,也就是说 .
公式
综上所述,我们最终得到以下公式:

执行案例
可以点此获取高度优化、生产就绪和许可 (MIT) 的 VRGDA 实施和各种发行时间表。
结论
VRGDA 提供了一种支持高度可定制化时间表发行 NFT 的方法,同时允许用户随时无缝地购买它们。
在 Art Gobblers 的案例中,它们使我们能够更好地定制和规划社区的增长和 UGC 动态。以 0xMonaco 为例,它创造了一个具有挑战性且竞争激烈的游戏循环。
我们相信在 NFT、GameFi、DeFi 等领域这一设计还有许多其他潜在应用。我们迫不及待地想看看你的创新了。
原文链接